Photo by niko photos

The Pruning Radix Trie is a novel data structure, derived from a radix trie — but 3 orders of magnitude faster.

After I published SymSpell, a very fast spelling correction algorithm, I have been frequently asked whether it can be used for auto-completion as well. Unfortunately, despite its speed, SymSpell is a poor choice for auto-complete. The Radix Trie seemed to be a natural fit for auto-complete. But the lookup of a small prefix in a large dictionary — resulting in an huge number of candidates — lacked in speed. Therefore I designed the Pruning Radix Trie - an auto-complete solution with the speed of SymSpell.

A Radix Trie or Patricia Trie is a space-optimized trie (prefix tree). A Pruning Radix trie is a novel Radix trie algorithm, that allows pruning of the Radix trie and early termination of the lookup.

In a Radix Trie the lookup is O(k), where k is the length of the key. While this is very fast, unfortunately this holds only true for a single term lookup. The lookup of all terms (or the top-k most relevant) for a given prefix is much more expensive — and this is the operation required for auto-complete.

Especially for short prefixes, we have to traverse a significant part of the whole tree in order to find all or to identify the top-k most relevant candidates.

A complete result set of millions of suggestions for a short prefix wouldn’t be helpful at all for auto-completion. That’s why in most cases we are not interested in a complete set of all children for a given prefix, but only in the top-k most relevant terms. We can utilize this fact to achieve a massive reduction of lookup time for top-k results. By augmenting the trie node data structure with additional information about the maximum rank of all its children we can then implement a pruning and early termination of the trie traversal.

The lookup acceleration is achieved by storing in each node the maximum rank of all its children. By comparing this maximum child rank with the lowest rank of the results retrieved so far, we can heavily prune the trie and do early termination of the lookup for non-promising branches with low child ranks.

UPDATE: In a Reddit comment there was the misconception that for top-10 suggestions one would need only 10 lookups in the dictionary. Beware, it’s not that simple! To get the top-10 most relevant auto-complete suggestions it is not enough to do just 10 lookups in the 6 million entry dictionary. In the default textbook implementation of a trie, for a 1-char prefix ‘m’ as input we have to traverse a significant part of the whole tree and evaluate all 459,735 candidates that start with ‘m’, because we don’t want just 10 random suggestions, but those with the highest rank (I use the word frequency count of the suggestion as rank). And that’s where the improvement of the Pruning Radix trie is. By storing and utilizing the maximum rank of all children of a node, we can massively prune the trie and do early termination. That allows us to reduce the number of nodes we have to traverse and we can reduce the number of candidates we have to evaluate from 459,735 to 110!

Dictionary

Terms.txt contains 6 million unigrams and bigrams derived from English Wikipedia titles, with term frequency counts used for ranking. But you can use any frequency dictionary for any language and domain of your choice.

Performance

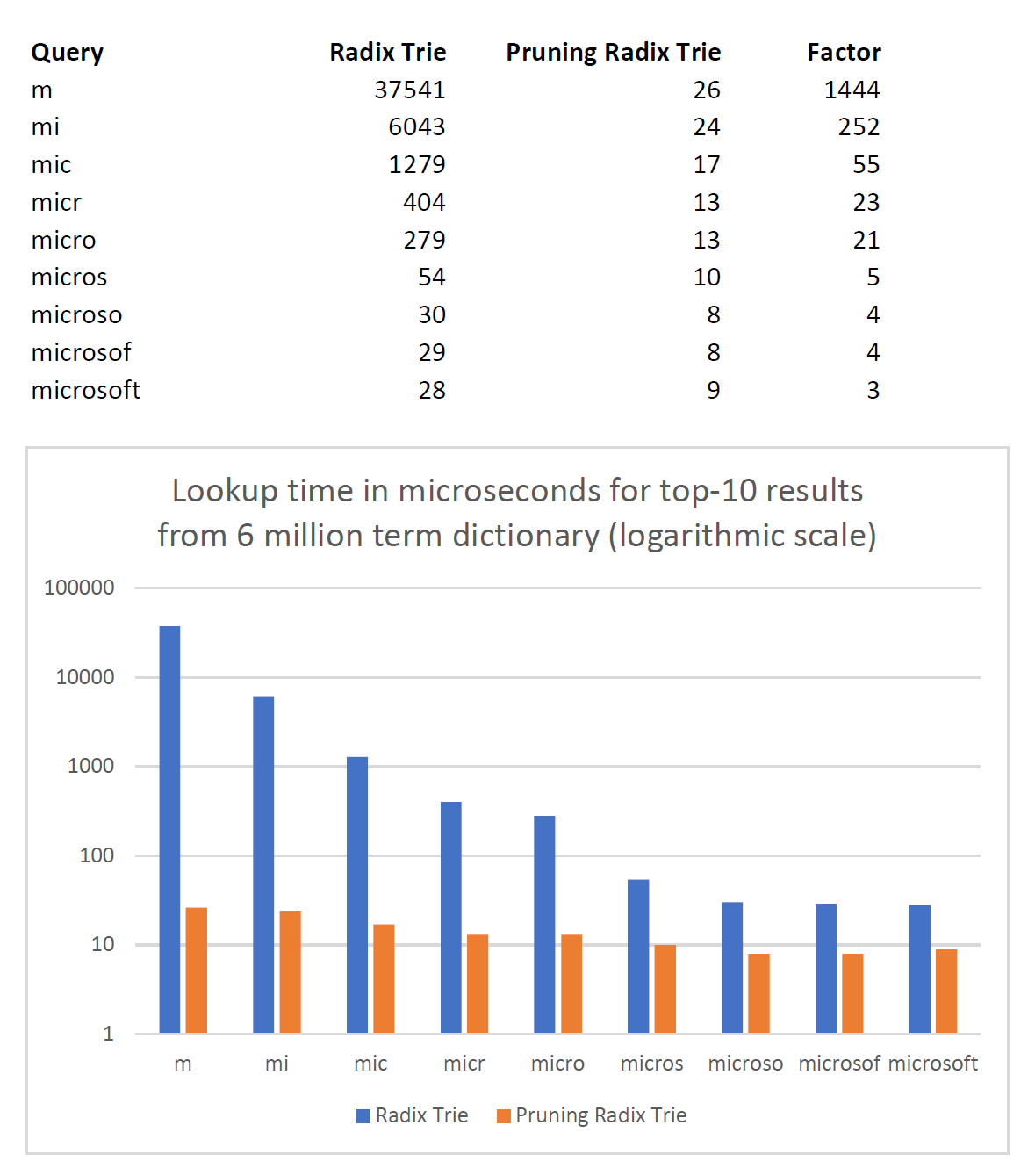
The Pruning Radix Trie is up to 1000x faster than an ordinary Radix Trie.

Application:

The PruningRadixTrie is perfect for auto-completion or query completion. While 37 ms for an auto-complete might seem fast enough for a single user, it becomes a completely different story if we have to serve thousands of users in parallel, e.g. in search engines and search as a service search API. Then autocomplete lookups in large dictionaries become only feasible when powered by something much faster than an ordinary radix trie.

Autocomplete vs. Spelling correction

Both concepts are related and somewhat similar. That’s why sometimes it is tempting to use a data structure designed to solve spelling correction also to use for auto-complete — and vice versa. But that’s not a good idea.

Misuse of spelling correction to achieve auto-complete

Usually, we expect from auto-complete to find the most likely word for any given prefix, even if the prefix is short and the complete word is long. Then the edit distance between input and output becomes large — which results in two problems when trying to use a spelling correction algorithm for auto-complete:

• the lookup time becomes infeasible huge, because the calculation of large edit distances with the Levenshtein algorithm is very time-consuming. Even an extremely fast spelling correction algorithm like SymSpell would have a hard time to return “Microsoft Windows” for a “mi” prefix within a reasonable time and without diluting the returned suggestions with thousands of meaningless candidates.
• The overwhelming number of returned candidates for a large maximum edit distance defeats the purpose of being helpful. As the maximum edit distance would be larger then the length of the given input prefix, most of the returned candidates would not have even a single letter in common with the input prefix.

Misuse of auto-complete for spelling correction

On the other hand, from spelling correction, we expect to correct all errors up to a maximum edit distance, even if the error occurs in the first letter. Then there is no common prefix at all, rendering the use of a trie (prefix tree) for spelling correction impossible.

Combination of auto-complete for spelling correction

Ultimately we can combine both algorithms e.g. in the query field of a search engine like SeekStorm. But how to do that efficiently, that’s another story.

Other options

There are other ways to speed-up auto-suggestion, alternatively to using a Pruning Radix Trie:

• Enabling auto-complete only above a prefix length threshold (e.g. ≥3), because the lookup time for a short prefix in a trie is especially high and the precision of suggestion candidates is low.
• Using a hash map with precalculated top-k suggestions for each prefix below a prefix length threshold (e.g. ≤3), because the lookup time for short prefix is especially high and number prefixes is limited and their the memory consumption in hash map manageable

Source Code

The C# code has been released as Open source under the MIT license on Github