Vergilius Vaticanus

TL;DR

Faster Word Segmentation by using a Triangular Matrix instead of Dynamic Programming. The integrated Spelling correction allows noisy input text. C# source code on GitHub.

For people in the West it seems obvious that words are separated by space, while in Chinese, Japanese, Korean (CJK languages), Thai and Javanese words are written without spaces between words.

Even the Classical Greek and late Classical Latin were written without those spaces. This was known as Scriptio continua.

And it seems we haven’t yet lost our capabilities: we can easily decipher

thequickbrownfoxjumpsoverthelazydog

as

the quick brown fox jumps over the lazy dog

Our brain does this somehow intuitively and unconsciously. Our reading speed slows down just a bit, caused by all the background processing our brain has to do. How much that really is we will see if we attempt to do it programmatically.

Why?

But why would we want to implement word segmentation programmatically, if people can read the unsegmented text anyway?

For CJK languages without spaces between words, it’s more obvious.

Web search engines like Google or Baidu have to index that text in a way that allows efficient and fast retrieval. Those web search engines are based on inverted indexes. During crawling for each word a separate list of links is created. Each list contains links to all web pages where that specific word occurs.

If we search for a single word then all links contained in the list are valid search results. If we do a boolean search (AND) for two words, then those two lists are intersected and only the links that are contained in both list are returned as results.

Spelling correction allows to correct misspelled words. This is done by looking up the possible misspelled word in a dictionary. If the word is found the word is deemed correct. If the word is not found then those words from the dictionary which are closest to the candidate (according to an edit distance metric like Damerau-Levenshtein) are presented as spelling correction suggestions. Of course, the naive approach of calculating the edit distance for each dictionary entry is very inefficient. SymSpell is a much faster algorithm. But anyway, the precondition is to identify the word boundaries first in order to have an input for the spelling correction algorithm in the first place.

Machine translation, Language understanding, Sentiment analysis and many other information processing tasks are also based on words.

But why would we need word segmentation for languages that already have spaces between words? Well, even in those languages that normally have spaces they get sometimes missing! There are surprisingly many application fields:

• Normalizing English compound nouns that are variably written: for example, ice box = ice-box = icebox; pig sty = pig-sty = pigsty) for search & indexing.
• Word segmentation für compounds: both original word and split word parts should be indexed.
• Typing errors may cause missing spaces.
• Conversion errors: during conversion, some spaces between word may get lost, e.g. by removing line breaks instead of replacing them with spaces.
• OCR errors: inferior quality of original documents or handwritten text may cause that not all spaces between words are recognized properly.
• Transmission errors: during the transmission over noisy channels spaces can get lost or spelling errors introduced.
• Keyword extraction from URL addresses, domain names, table column description or programming variables that are written without spaces.
• For password analysis, the extraction of terms from passwords can be required.
• Speech recognition, if spaces between words are not properly recognized in spoken language.
• Automatic CamelCasing of programming variables.

But word segmentation might be of interest also beyond Natural languages, e.g. for segmenting DNA sequence into words (PDF).

Segmentation variant generation

A string can be divided in several ways. Each distinct segmentation variant is called a composition. How many different compositions exist?

• In a string of length n the number of potential word boundaries is n’=n-1 (between every char of the string).
• Each of those positions can actually be used as word boundary or not. We can think of this as a number in binary form, where each bit can be set or not.
• In the binary numeral system a number with n digits can represent x=2^n distinct numbers. Therefore the number of segmentation variants is also x=2^n’ (n’ number of potential word boundaries)
• Each string of length n can be segmented into 2^n−1 possible compositions.

The compositions of the string have to be evaluated for two criteria:

• Whether the composition is a valid word segmentation, i.e. it consist of genuine words (we will learn how to deal with unknown words).
• Which of the valid word segmentations (there might exist several) for that specific input string has the highest probability and will be selcected as final result.

Recursive approach

The naive approach would be to generate all possible variants to segment a string into substrings (word candidates) and lookup those candidates in a dictionary. Those segmentation variants where all substrings are a valid word are returned as results.

The following recursive algorithm enumerates all compositions:

For “isit” as input it will generate all 8 possible compositions:

1
2
3
4
5
6
7
8
i s i t
i s it
i si t
i sit    <--
is i t
is it    <--
isi t
isit

Two of the compositions consist of genuine English words and would be valid segmentation suggestions. In section segmentation variant selection we will learn how to determine which of the two variants is more likely.

But there is a problem. Each string of length n can be segmented into 2^n−1 possible compositions. This is huge!

The naive algorithm is exponential and will not scale for longer strings!

E.g. our string thequickbrownfoxjumpsoverthelazydog has a length of 35. This results in more than 17 billion segmentation variants to be generated, all their words to be verified in the dictionary, and finally, the variants to be ranked by probability.

We don’t usually have so much time and computing power. We need to come up with something smarter and more efficient.

Incremental Calculation of Local Optimum

We don’t need to generate all compositions in order to find the best one!

In the naive algorithm, the whole tree of segmentation variants is generated. For repeating substrings the segmentation is also generated repeatedly. And only at the end, all generated complete segmentations are compared to find the best one.

But each specific substring we need to segment only once. We calculate the best partial segmentations for each substring just once and reuse it during the incremental segmentation of the whole input string.

The selection of a local optimum is based on the assumption that consecutive partial segmentations are independent.

Calculating the optimum segmentation of each substring only once and reusing it saves a lot of time and memory otherwise required for generating and storing repetitive patterns.

Two different approaches to achieve this are presented in the next sections.

Dynamic programming approach

One way of improving the algorithm is using Dynamic programming:

This a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions. The next time the same subproblem occurs, instead of recomputing its solution, one simply looks up the previously computed solution, thereby saving computation time. Each of the subproblem solutions is indexed in some way, typically based on the values of its input parameters, so as to facilitate its lookup. The technique of storing solutions to subproblems instead of recomputing them is called “memoization”.[Source: Wikipedia]

Every time before our program makes a recursive call to segment the remaining string we check whether this exact substring has been segmented before. If so we just dismiss the recursive call and retrieve the optimum segmentation result for that exact substring from a cache (where it has been stored the first time that specific substring has been segmented).

That technique has been used for word segmentation several times:

• Peter Norvig’s word segmentation Python code can be found in the chapter Natural Language Corpus Data of the book Beautiful Data
• Grant Jenks python_wordsegment.
• Jeremy Kun word segmentation

As I couldn’t find a C# port on the Web, here is my implementation of the Dynamic Programming approach:

WordSegmentationDP source code

Triangular Matrix approach

The Dynamic Programming approach used recursion and a dictionary for the Memoization of the optimum segmentation of remainder substrings.

The Triangular Matrix approach uses nested loops and a Circular Array to store the optimum segmentation of prefix substrings instead.

A Triangular Matrix of parts with increasing lengths is generated, organized as Circular Array. This allows a constant O(1) memory consumption (vs. linear O(n) for Dynamic Programming), as intermediate segmentation variants are overwritten, once they are not longer required. Instead of storing full segmented strings, only a bit vector of potential space positions is used. This reduces the memory consumption to store segmentation variants (1 bit instead of 1 char) and is Garbage Collection friendly.

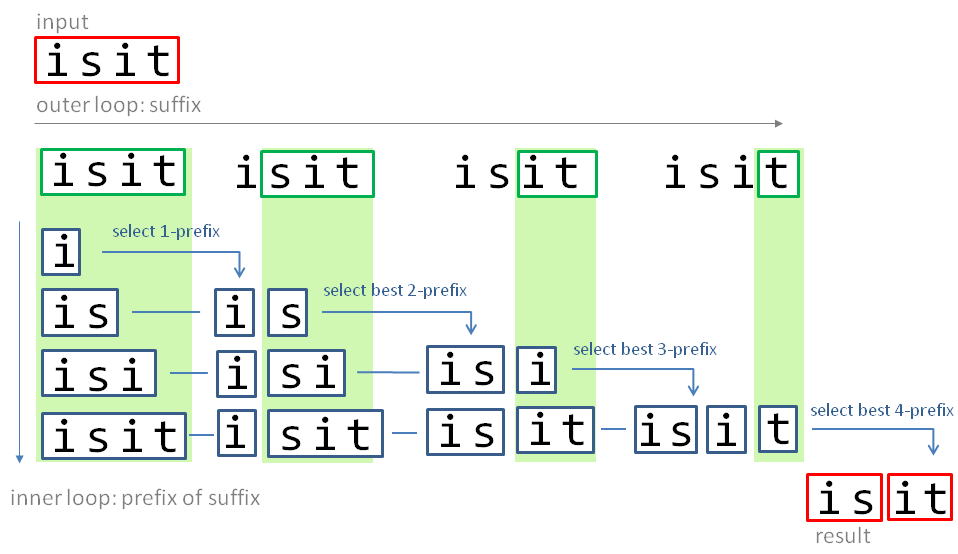Triangular Matrix algorithm

And the C# implementation of the Triangular Matrix approach:

WordSegmentationTM source code

Dynamic Programming vs. Triangular Matrix

So, what are the similarities and the differences between the two approaches?

• Both algorithms provide identical results.
• Both have the same linear computational complexity of O(n).
• Both store the best segmentation variant for a specific substring, so that it has to be calculated only once.
• DP calculates all segmentation variants for a specific remainder substring consecutively. The best variant is stored in a cache dictionary (hash table). To access the segmentation result for a specific remainder the substring is used as the key.
• TM calculates the segmentation variants for a specific prefix substring non-consecutively, at a specific position of the inner loop. The best variant is stored in an array. To access the segmentation result for a specific prefix substring the loop position is used as the index.
• TM has a constant memory consumption (array size = O(1) = maxSegmentationWordLength), while DP has a linear memory consumption (number of cache dictionary entries = O(n) = input text length).
• Additionally, even for the same number of entries the memory consumption of an array (MT) is lower than the memory consumption of a dictionary (DP).
• Additionally, TM stores only a bit vector of potential space positions, while DP stores full segmented strings. This further reduces the memory consumption to store segmentation variants (1 bit instead of 1 char) and is Garbage Collection friendly.
• The access to the array via index (MT) is faster than the access to the cache dictionary via key (DP).
• The lookup number to the word frequency dictionary is similar for both.
• Iteration is usually faster than recursion and prevents possible recursion limits (exceeding maximum recursion depth / stack overflow).

In my benchmark, the Triangular Matrix approach was 2x faster than the Dynamic Programming approach. It has a lower memory consumption, better scaling and is GC friendly.

Originally I thought the two approaches to be completely different. But after comparing their characteristics I believe that the Triangular Matrix approach is just a special form of Dynamic Programming that uses an circular array instead of a dictionary for memorization, loops instead of recursion and incrementally optimizes prefix strings instead of remainder strings.

Maximum word length

Word candidates are generated from a string only up to a maximum length. Norvig had chosen the maximum word length arbitrarily to 20. As the longest word is language dependent (with 6 characters maximum in Chinese) it is better to derive it from the longest word present in the dictionary. While this is heuristic, it is very unlikely that a valid genuine word exists which is larger than the longest contained in the dictionary. It also prevents looking up words which we already know to be not in the dictionary and creating compositions that contain such non-existing words. This will ensure a maximum segmentation speed.

Computational Complexity

Both the Dynamic Programming and the Triangular Matrix approach have a linear runtime O(n) to find the optimum composition.

The exact relationship between text length n and runtime is O(n * Min(n, maximum dictionary word length) / 2).

Segmentation variant selection

There might be several valid variants to split a string into words though:

isit might be i sit or is it

Word frequencies (or word occurrence probabilities) are used to determine the most likely segmentation variant.

Word occurrence probability P=word count C / corpus size N

Corpus size N is the total number of words in the text corpus used to generate the frequency dictionary. N equals the sum of all counts c in the frequency dictionary only if the dictionary is complete, but not if the dictionary is truncated or filtered.

Naive Bayes Rule

We assume the word probabilities of two words to be independent. Therefore the Naive Bayes probability of the word combination is the product of the two word probabilities:

P(AB)=P(A) * P(B)

The segmentation quality can be further improved by the use of of bigram probabilities instead of single word probabilities.

Logarithmic scale

Instead of computing the product of probabilities we are computing the sum of the logarithm of probabilities. Because the probabilities of words are about 10^-10, the product of many such small numbers could exceed (underflow) the floating number range and become zero.

log(P(AB))=log(P(A))+log(P(B))

Known words

In order to calculate the word occurrence probabilities we can use different approaches:

• Create our own word frequency dictionary by counting the words in a large text corpus. If the dictionary is derived from a corpus similar to the documents you will process, the similar word occurrence probabilities distribution will ensure optimum results.
• Use an existing frequency dictionary which contains word counts, e.g. the Google Books Ngram data. The drawback is that Google Books Ngram data contains not only valid words but also spelling errors and other fragments. While many spelling errors will anyway have no influence due to their low probabilities, that is not always guaranteed. E.g. frequent spelling errors of frequent words could win over genuine rare words.
• Dictionary quality is paramount for segmentation quality. In order to achieve this two data sources can be combined by intersection: The huge Google Books Ngram data provides representative word frequencies (but contains many entries with spelling errors) even for rare words and SCOWL — Spell Checker Oriented Word Lists which ensures genuine English vocabulary (but contained no word frequencies required for ranking of suggestions within the same edit distance).

I have decided to use variant 3, the intersection of a genuine English word dictionary with word frequencies from the Google Books Ngram corpus because of the relevant word frequencies even for rare words. But the drawback compared to variant 1 is that the Google corpus was derived from books from different centuries. The use of languages has been changed over time, and the use of language is different in different domains (e.g. medicine, law, prose, news, science).

Unknown words

We can’t fully rely on a dictionary. No dictionary will be ever complete. There are uncommon words, new words, foreign words, personal names, brand names, product names, abbreviations, informal words, slang and spelling errors. Even for words not contained in the dictionary, we want the word segmentation algorithm to select the best possible segmentation variant.

Therefore we have to estimate a word occurrence probability to unknown words. The information we have even for unknown words is their length.

George Kingsley Zipf observed that the length of words is inversely related to their frequency. Words that are used often, such as “the,” tend to be short (Zipf G. The Psychobiology of Language). Zipf explained this with the “Principle of Least Effort” ( Zipf G. Human Behavior and the Principle of Least Effort).

The following formula to calculate the probability of an unknown word has been proposed by Peter Norvig in Natural Language Corpus Data, page 224:

Approximate word occurrence probability P=10 / (N * 10^word length l)

We have to be aware that this is a raw estimation which contains heuristic parameters, which might have to be adjusted for languages other than English. More information about the relation of word length and word frequency can be found in “Length-frequency statistics for written English” by Miller, Newmann, Friedmann and for the aspect of different languages in “Word Length and Word Frequency” by Strauss, Grzybek, Altmann.

Of course we could think of more sophisticated probability calculation, e.g. by using Markov chains or known prefixes and suffixes to estimate the probability of a specific substring to be a genuine word. That would make it even possible to segment consecutive unknown words correctly.

Languages

The word segmentation algorithm itself is language independent. But the word frequency dictionary is language specific. In order to word segment text written in a certain language a frequency dictionary for that exact language is required. The Google Books n-gram data includes word frequencies for many languages. Also, as mentioned above, the formula to estimate the probability for unknown words depending on their length contains heuristic parameters, which have to be adjusted for each language individually to obtain optimum segmentation results.

Word segmentation and spelling correction

As mentioned above several word segmentation solutions exist.

SymSpell.WordSegmentation combines word segmentation and spelling correction.

During segmentation many potential word candidates are generated — all of them need to be spell checked and the suggestion candidates to be ranked.

This has been only feasible by utilizing the extreme lookup speed of SymSpell:

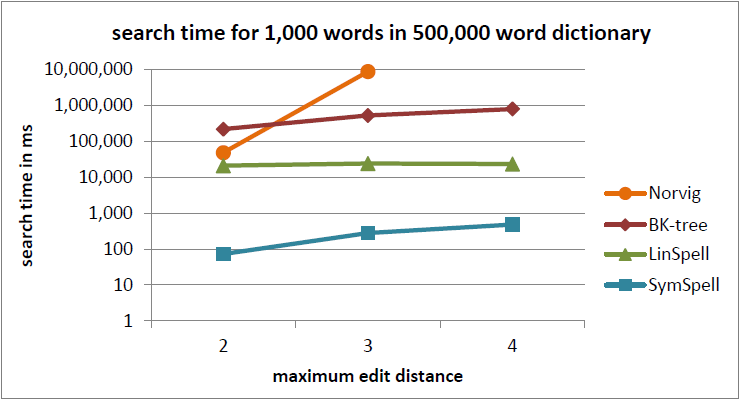
By a parameter for maximum edit distance, we can control how much spelling correction we want to allow. With maxEditDistance=0 we have pure word segmentation without spelling correction. With maxEditDistance=2 we consider all words from the dictionary as valid candidates for a substring if they are within a Damerau-Levenshtein edit distance ≤2.

Higher maximum edit distance allows to correct more errors, but comes at the cost of false-positive corrections and lower segmentation performance. The actual trade-off depends on the quality of the input material. It can make buggy input readable, but it can also introduce errors into an otherwise perfect input.

Example 1

1
2
3
4
5
6
input:                 isit
Norvig segment:        is it             -> no spelling correction
WordSegmentation ed=0: is it             -> no spelling correction
WordSegmentation ed=1: visit             -> spelling correction       <--
LookupCompound ed=0:   i sit             -> no spelling correction
LookupCompound ed=1:   visit             -> spelling correction       <--

** Example 2**

1
2
3
4
5
6
input:                 independend
Norvig segment:        in depend end      -> no spelling correction
WordSegmentation ed=0: in depend end      -> no spelling correction
WordSegmentation ed=1: independent        -> spelling correction      <--
LookupCompound ed=0:   independend        -> no spelling correction
LookupCompound ed=1:   independent        -> spelling correction      <--

Example 3

1
2
3
4
5
6
input:                 whocouqdn’tread
Norvig segment:        who couqdn’t read  -> no spelling correction
WordSegmentation ed=0: who co uqdn’t read -> no spelling correction
WordSegmentation ed=1: who couldn’t read  -> segmentation+correction  <--
LookupCompound ed=0:   whocouqdn’tread    -> more than 1 space/token
LookupCompound ed=1:   whocouqdn’tread    -> more than 1 space/token

• In order to make algorithms comparable for SymSpell.WordSegmentation and Norvig’s word segmentation the same frequency dictionary has been used.

WordSegmentation vs. LookupCompound

The SymSpell spelling correction and fuzzy search library comes with a method LookupCompound. It supports compound aware automatic spelling correction of multi-word input strings with three cases:

1. mistakenly inserted space within a correct word led to two incorrect terms
2. mistakenly omitted space between two correct words led to one incorrect combined term
3. multiple input terms with/without spelling errors

Splitting errors, concatenation errors, substitution errors, transposition errors, deletion errors and insertion errors can be mixed within the same word.

So, what’s the difference then between SymSpell.WordSegmentation and SymSpell.LookupCompound, and what is similar?

• Both can insert and remove spaces from multi-word input strings, as well as correct spelling errors.
• LookupCompound can insert only a single space into a token (string fragment separated by existing spaces). It is intended for spelling correction of word segmented text but can fix an occasional missing space. There are fewer variants to generate and evaluate because of the single space restriction per token. Therefore it is faster and the quality of the correction is usually better.
• WordSegmentation can insert as many spaces as required into a token. Therefore it is suitable also for long strings without any space. The drawback is a slower speed and correction quality, as many more potential variants exist, which need to be generated, evaluated and chosen from.

Application

Word segmentation of text in CJK languages or noisy text is a part of the text processing pipelines of search engines and search as a service search API where you have to index thousands of documents per second. Where word segmentation is not even the main processing task, but only one of many components in text preprocessing, you need the fastest word segmentation algoritm you can get.

Source Code

Word Segmentation without Spelling Correction:

WordSegmentationTM and WordSegmentationDP and are released on GitHub as Open Source under the MIT license.

Word Segmentation with Spelling Correction:

WordSegmentation and LookupCompound are part of the SymSpell library and released on GitHub as Open Source under the MIT license.